Skip to main content

Colliders

Colliders represent the geometric shapes that generate contacts and collision events when they touch. Attaching one or multiple colliders to a rigid body allow the rigid-body to be affected by contact forces.

Creation and insertion​

A collider is created by a ColliderBuilder structure that is based on the builder pattern. Then it needs to be inserted into the ColliderSet that will be processed by the physics-pipeline, collision-pipeline, or query-pipeline.

info

The following example shows several setters that can be called to customize the collider being built. The input values are just random so using this example as-is will not lead to a useful result.

use rapier2d::prelude::*;
use std::f32::consts::PI;

// The set that will contain our colliders.
let mut collider_set = ColliderSet::new();

// Builder for a ball-shaped collider.
let _ = ColliderBuilder::ball(0.5);
// Builder for a cuboid-shaped collider.
let _ = ColliderBuilder::cuboid(0.5, 0.2);
// Builder for a capsule-shaped collider. The capsule principal axis is the `x` coordinate axis.
let _ = ColliderBuilder::capsule_x(0.5, 0.2);
// Builder for a capsule-shaped collider. The capsule principal axis is the `y` coordinate axis.
let _ = ColliderBuilder::capsule_y(0.5, 0.2);
// Builder for a triangle-mesh-shaped collider.
let _ = ColliderBuilder::trimesh(vertices, indices);
// Builder for a heightfield-shaped collider.
let _ = ColliderBuilder::heightfield(heights, scale);
// Builder for a collider with the given shape.
let collider = ColliderBuilder::new(SharedShape::ball(0.5))
    // The collider translation wrt. the body it is attached to.
    // Default: the zero vector.
    .translation(vector![1.0, 2.0])
    // The collider rotation wrt. the body it is attached to.
    // Default: the identity rotation.
    .rotation(PI)
    // The collider position wrt. the body it is attached to.
    // Default: the identity isometry.
    .position(Isometry::new(vector![1.0, 2.0], PI))
    // The collider density. If non-zero the collider's mass and angular inertia will be added
    // to the inertial properties of the body it is attached to.
    // Default: 1.0
    .density(1.3)
    // The friction coefficient of this collider.
    // Default: ColliderBuilder::default_friction() == 0.5
    .friction(0.8)
    // Whether this collider is a sensor.
    // Default: false
    .sensor(true)
    // All done, actually build the collider.
    .build();

// Insert the collider into the set, without attaching it to a rigid-body.
let collider_handle = collider_set.insert(collider.clone());

let mut rigid_body_set = RigidBodySet::new();
let rigid_body_handle = rigid_body_set.insert(RigidBodyBuilder::dynamic().build());
// Or insert the collider into the set and attach it to a rigid-body.
let handle = collider_set.insert_with_parent(collider, rigid_body_handle, &mut rigid_body_set);

Collider type​

There are two types of colliders:

  • ColliderType::Solid: solid colliders represents a geometric shape that can have contact points with other colliders to generate contact forces to prevent objects from penetrating-each-others.
  • ColliderType::Sensor: sensor colliders on the other end don't generate contacts: they only generate intersection events when one sensor collider and another collider start/stop touching. Sensor colliders are generally used to detect when something enters an area. Note that, for symmetry with non-sensor colliders, sensors do contribute to the mass of a rigid-body they are attached to.

By default a collider is a solid collider. This can be changed to a sensor when constructing the collider, or after its construction:

/* Set the collider type when the collider is created. */
let collider = ColliderBuilder::ball(0.5).sensor(true).build();
/* Set the collider type after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_sensor(true);
assert!(collider.is_sensor());

Shapes​

Overview​

The main characteristic of a collider is its geometric shape. The supported shapes are illustrated bellow:

supported shapes

Shapes only hold information about their geometry. Their world-space position is given by the collider's position. Balls, cuboids, capsules, cylinders, and cones are all described by their half-height and/or radius. Compound shapes, convex meshes, triangle meshes, heightfields, and polylines are more complicated shapes described in the next paragraphs.

Convex meshes​

A convex mesh is a shape such that, if two points are part of the shape, then the segment between these two points is also part of the shape:

convex versus non-convex

There are two ways of creating a collider with a convex shape:

  1. Using ColliderBuilder::convex_hull(points). This is the simplest approach: it will automatically compute the convex hull of the given set of points. A convex hull is the smallest convex shape that contains all the given points.
  2. Using ColliderBuilder::convex_mesh(points, indices) in 3D or ColliderBuilder::convex_polyline(points) in 2D. This takes a mesh described by its vertex buffer and index buffer and assumes it is already convex (you need to ensure that it is convex yourself). This will be more efficient than the ColliderBuilder::convex_hull constructor because it won't perform any calculations to ensure convexity. However, if the input mesh isn't actually convex, the collision-detection for that shape will give an incorrect result.

Triangle meshes and polylines​

Triangle meshes (in 3D) and polylines (in 2D) can be used to describe the boundary of any kind of shape. This is generally useful to describe the fixed environment in games (terrains, buildings, etc.) Triangle meshes and polylines are defined by their vertex buffer and their index buffer. The winding of the triangles of a triangle mesh does not matter. Its topology doesn't matter either (it can have holes, cavities, doesn't need to be closed or manifold). It is however strongly recommended to avoid triangles that are long and thin because they can result in a lower numerical stability of collision-detection.

note

A triangle mesh/polyline is composed of triangles/segments with no thickness. This means that geometric queries like point-containment tests won't work intuitively because the triangle mesh is assumed to have no interior.

A triangle-mesh collider can be built with ColliderBuilder::trimesh(vertices, indices) where vertices is the buffer containing all the vertices of the mesh, and indices is a set of indices indicating what vertex is used by what triangle. The vertex buffer and index buffer may have different lengths, and any vertex can be shared by multiple triangles.

A polyline collider can be built with ColliderBuilder::polyline(vertices, indices) where vertices is the buffer containing all the vertices of the polyline, and indices is an optional set of indices indicating what vertex is used by what segment. The vertex buffer and index buffer may have different lengths, and any vertex can be shared by multiple segments. If the given vertex buffer is None then the input vertices are assumed to form a line strip, i.e., the polyline is formed from the segments [vertices[0], vertices[1]], [vertices[1], vertices[2]], etc.

warning

It is discouraged to use a triangle meshes or a polylines for colliders attached to dynamic rigid-bodies. Because they have no interior, it is easy for another object to get stuck into them. In order to simulate properly non-convex objects, it is recommended to use a convex decomposition with a compound shape instead.

Heightfields​

heightfield

Heightfields are a more restrictive version of triangle-meshes and polylines. However, they can be easier to define and use much less memory. Therefore heightfields are useful to define large parts of terrains with simple topologies.

A 3D heightfield is basically large rectangle in the X-Z plane, subdivided in a grid pattern at regular intervals. Each vertex of this subdivision is given a height, i.e., the coordinate of that point along the Y axis. A 3D heightfield collider can be created with ColliderBuilder::heightfield(heights, scale) where heights is a matrix indicating the altitude of each subdivision point of that heightfield. The number of rows of that matrix is the number of subdivision along the X axis, and the number of columns is the number of subdivision along the Z axis. The scale argument indicates the size of the rectangle of the X-Z plane.

info

A heightfield collider can be given any orientation by changing the orientation of the collider itself.

A 2D heightfield is a large segment along the X axis, subdivided at regular intervals. Each vertex of this subdivision is given a height, i.e., the coordinate of that point along the Y axis. A 2D heightfield collider can be created with ColliderBuilder::heightfield(heights, scale) where heights is a vector indicating the altitude of each subdivision point of that heightfield. The number of elements on that vector is the number of subdivision of the heightfield. The scale argument indicates the length of the subdivided segment along the X axis.

Compound shapes​

It is not recommended to use a triangle mesh or polyline for the shape of a collider attached to a dynamic rigid-body. The alternative is to use a compound shape to model a non-convex object as the union of multiple convex parts (which can be cuboids, balls, convex meshes, etc.) This is commonly known as a convex decomposition.

info

An alternative to using a compound shape is to attach multiple colliders to the same rigid-body: all the colliders will move with the rigid-body automatically, behaving in a very similar way than using a single collider with a compound shape. The main differences between the two approaches is about collision events: each collider generates individual collision start/stop events.

To build a compound shape, it is possible to directly provide the set of shapes as well as their position in the compound shape's local space:

let _ = ColliderBuilder::compound(vec![(pos1, shape.clone()), (pos2, shape.clone())]);

It is also possible to build a compound shape modelling the convex decomposition of a 3D triangle mesh or 2D polyline using the ColliderBuilder::convex_decomposition(vertices, indices) method. This will automatically create a compound shape composed of multiple convex meshes obtained from the approximate convex decomposition of the triangle mesh (or polyline in 2D) using the VHACD algorithm. Here are examples of a 2D concave polygon decomposed into two convex parts as well as a 3D mesh with its approximate convex decomposition composed of 7 convex parts:

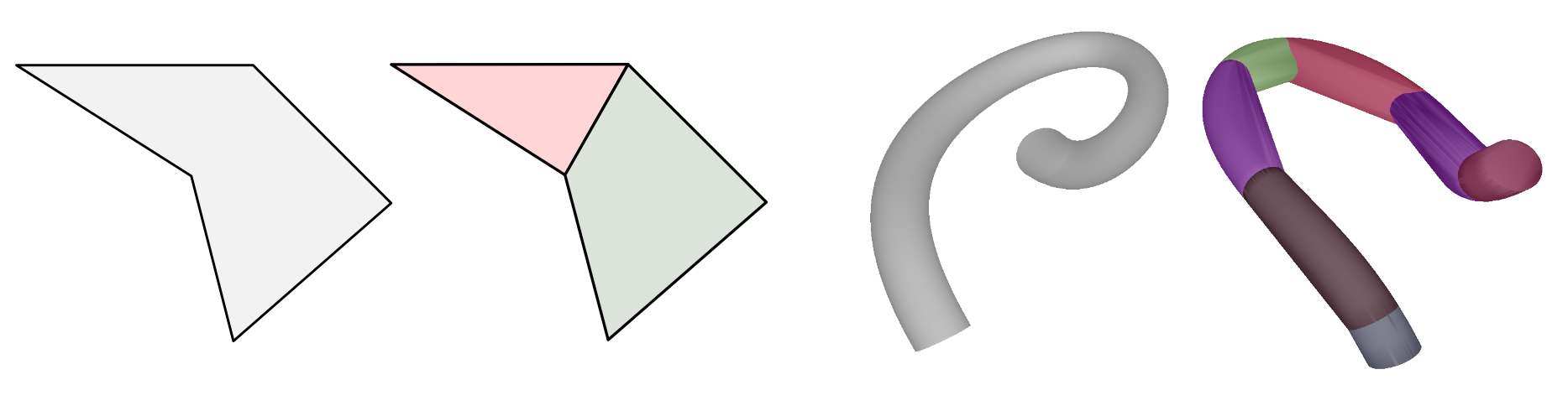
convex decomposition

Round shapes​

Some shapes have round variants: RoundCuboid, RoundCylinder, RoundCone, RoundConvexPolygon and RoundConvexPolyhedron. These are shapes to which is added a small thickness with round border:

round cuboid

note

For algorithmic reasons, collision-detection involving round cylinders, round cones, round convex polygon or round convex polyhedron will be faster than collision-detection with their non-round counterparts. However, collision-detection with round-cuboids will be slower than collision-detection with regular cuboids.

Colliders with round shapes are built in a way very similar to their non-round counterparts, e.g., ColliderBuilder::round_cuboid. These constructors take one additional parameter: the size of the added thickness called border_radius.

Mass properties​

The mass properties of a rigid-body is computed as the sum of the mass-properties manually set by the user for the rigid-body, plus the mass-properties of the colliders attached to it. There are two ways to define the mass-properties of a collider:

  1. The easiest, automatic, way: by giving the collider a non-zero density (the default density is 1.0) or a non-zero mass. This will make sure the other mass-properties like the angular inertia tensor are computed automatically from the collider's shape.
  2. The manual way: by giving an explicit mass and angular inertia to the collider.

It is recommended to use the density-based or mass-based approaches as it will ensure the automatically-computed mass-properties are coherent with the geometric shape. Wrong mass-properties (especially the angular inertia part and center-of-mass location) may lead to odd behaviors. The manual approach is usually useful when modeling real-world objects for which you already know the real-world mass, center-of-mass, and angular inertia tensor.

The mass-properties of a collider can only be set when the collider is created:

let rigid_body = RigidBodyBuilder::dynamic().build();
let rigid_body_handle = rigid_body_set.insert(rigid_body);
// First option: by setting the density of the collider (or we could just leave
//               its default value 1.0).
let collider = ColliderBuilder::cuboid(1.0, 2.0).density(2.0).build();
// Second option: by setting the mass of the collider.
let collider = ColliderBuilder::cuboid(1.0, 2.0).mass(0.8).build();
// Third option: by setting the mass-properties explicitly.
let collider = ColliderBuilder::cuboid(1.0, 2.0)
    .mass_properties(MassProperties::new(point![0.0, 1.0], 0.5, 0.3))
    .build();
// When the collider is attached, the rigid-body's mass and angular
// inertia is automatically updated to take the collider into account.
collider_set.insert_with_parent(collider, rigid_body_handle, &mut rigid_body_set);

Position​

The position of a collider represents its location (translation) in 2D or 3D world-space as well as its orientation (rotation). Its translational part is represented as a vector and its rotational part as an unit quaternion (in 3D) or a unit complex number (in 2D). Both are combined into an isometry.

warning

Please read carefully the paragraph after the next example. It explains how the collider position (and the action of setting this position) behaves differently when it is attached to a rigid-body.

It is possible to set this position when the collider is created or after its creation:

/* Set the collider position when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .translation(vector![1.0, 2.0])
    .rotation(0.4)
    // Set both translation and rotation at once.
    .position(Isometry::new(vector![1.0, 2.0], 0.4))
    .build();
/* Set the collider position after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_translation(vector![1.0, 2.0]);
collider.set_rotation(UnitComplex::new(0.4));
// Set both the translation and rotation at once.
collider.set_position(Isometry::new(vector![1.0, 2.0], 0.4));
assert_eq!(*collider.translation(), vector![1.0, 2.0]);
assert_eq!(collider.rotation().angle(), 0.4);

If a collider is attached to a rigid-body, its position is automatically updated by the physics pipeline when a rigid-body is moved by the physics pipeline. If a change to the rigid-body position is made by the user then the collider position will be updated during the next timestep.

Therefore, directly setting the position of a collider attached to a rigid-body will have no lasting effect. Instead, it is possible to set the position of the collider relative to the rigid-body it is attached to:

let rigid_body = RigidBodyBuilder::dynamic().build();
let rigid_body_handle = rigid_body_set.insert(rigid_body);
let collider = ColliderBuilder::ball(0.5)
    .translation(vector![1.0, 2.0])
    .build();
// Attach the collider to the rigid-body. The collider's position wrt. the rigid-body
// is automatically set to the collider current position when this method is called.
collider_set.insert_with_parent(collider, rigid_body_handle, &mut rigid_body_set);
/* Set the collider position wrt. its parent after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_position_wrt_parent(Isometry::translation(1.0, 2.0));
assert_eq!(
    collider.position_wrt_parent().unwrap().translation.vector,
    vector![1.0, 2.0]
);

Friction​

Friction is a force that opposes the relative tangential motion between two rigid-bodies with colliders in contact. This force has a direction orthogonal to the contact normal and opposite to the relative rigid-body motion at the contact point. Following the Coulomb friction model, the maximum magnitude of this force is the magnitude of the force along the contact normal multiplied by a friction coefficient. A friction coefficient of 0 implies no friction at all (completely sliding contact) and a coefficient greater or equal to 1 implies a very strong friction. Values greater than 1 are allowed.

note

Rapier does not make any distinction between the fixed and dynamic friction coefficients currently.

Each collider has its own friction coefficient. This means that when two colliders are in contact, we need to apply a rule that combines the friction coefficients of these two colliders into a single coefficient that will be used for the contact. This rule is described by the CoefficientCombineRule enum:

  • CoefficientCombineRule::Average: the average of the two coefficients is used for the contact.
  • CoefficientCombineRule::Min: the minimum among the two coefficients is used for the contact.
  • CoefficientCombineRule::Multiply: the product of the two coefficients is used for the contact.
  • CoefficientCombineRule::Max: the maximum among the two coefficients is used for the contact.

By default, the Average rule is used. Each collider can be given its own friction combine rule. When two colliders are in contact, we need to select one of their combine rule. The following precedence is used: Max > Multiply > Min > Average.

For example if one collider with the Multiply friction combine rule is in contact with a collider with the Average friction combine rule, then the Multiply rule will be applied for the friction coefficient of this contact (i.e. the coefficients of both colliders will be multiplied to obtain the coefficient used by the contact).

info

The CoefficientCombineRule system exists to cover a wide variety of use-cases efficiently. If this is not flexible enough, it is possible to get full control over the selection of friction coefficients for each contact point using contact modification. For example, contact modification allows the simulation of colliders with non-uniform friction coefficients.

The friction coefficient and friction combine rule can both be set when the collider is created or after its creation:

/* Set the friction coefficient and friction combine rule
when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .friction(0.7)
    .friction_combine_rule(CoefficientCombineRule::Min)
    .build();
/* Set the friction coefficient and friction combine rule
after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_friction(0.7);
collider.set_friction_combine_rule(CoefficientCombineRule::Min);
assert_eq!(collider.friction(), 0.7);
assert_eq!(
    collider.friction_combine_rule(),
    CoefficientCombineRule::Min
);

Restitution​

Restitution controls how elastic (aka. bouncy) a contact is. The elasticity of a contact is controlled by the restitution coefficient. A restitution coefficient set to 1 (fully elastic contact) implies that the exit velocity at a contact has the same magnitude as the entry velocity along the contact normal: it is as if you drop a bouncing ball and it gets back to the same height after the bounce. A restitution coefficient set to 0 implies that the exit velocity at a contact will be zero along the contact normal: it's as if you drop a ball but it doesn't bounce at all.

note

The friction and restitution coefficients are both managed in very similar ways: with the CoefficientCombineRule or with contact modification. The paragraph bellow is almost identical to the paragraph about friction.

Each collider has its own restitution coefficient. This means that when two colliders are in contact, we need to apply a rule that combines the restitution coefficients of these two colliders into a single coefficient that will be used for the contact. This rule is described by the CoefficientCombineRule enum:

  • CoefficientCombineRule::Average: the average of the two coefficients is used for the contact.
  • CoefficientCombineRule::Min: the minimum among the two coefficients is used for the contact.
  • CoefficientCombineRule::Multiply: the product of the two coefficients is used for the contact.
  • CoefficientCombineRule::Max: the maximum among the two coefficients is used for the contact.

By default, the Average rule is used. Each collider can be given its own restitution combine rule. When two colliders are in contact, we need to select one of their combine rule. The following precedence is used: Max > Multiply > Min > Average.

For example if one collider with the Multiply restitution combine rule is in contact with a collider with the Average restitution combine rule, then the Multiply rule will be applied for the restitution coefficient of this contact (i.e. the coefficients of both colliders will be multiplied to obtain the coefficient used by the contact).

info

The CoefficientCombineRule system exists to cover a wide variety of use-cases efficiently. If this is not flexible enough, it is possible to get full control over the selection of restitution coefficients for each contact point using contact modification. For example, contact modification allows the simulation of colliders with non-uniform restitution coefficients.

The restitution coefficient and restitution combine rule can both be set when the collider is created or after its creation:

/* Set the restitution coefficient and restitution combine rule
when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .restitution(0.7)
    .restitution_combine_rule(CoefficientCombineRule::Min)
    .build();
/* Set the restitution coefficient and restitution combine rule
after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_restitution(0.7);
collider.set_restitution_combine_rule(CoefficientCombineRule::Min);
assert_eq!(collider.restitution(), 0.7);
assert_eq!(
    collider.restitution_combine_rule(),
    CoefficientCombineRule::Min
);

Collision groups and solver groups​

The most efficient way of preventing some pairs of colliders from interacting with each other is to use collision groups or solver groups. Each collider is given:

  • A collision_groups for filtering what pair of colliders should have their contacts (or intersection test if at least one of the colliders is a sensor) computed by the narrow-phase. This filtering happens right after the broad-phase, at the beginning of the narrow phase.
  • A solver_groups for filtering what pair of colliders should have their contact forces computed. This filtering happens at the end of the narrow-phase, before the constraints solver.

In other words, the solver_groups is here to prevent contact forces from being computed between some colliders, whereas the collision_groups will also prevent the contact themselves (and contact events) from being computed. The collision_groups should be preferred most of the time because it skips more computations. The solver_groups is only useful if you really want the contact information to be computed but not the forces, for example so that you can apply your own forces based on these contacts.

A collision group or solver group is described as a pair of bit masks:

  • The groups membership indicates what groups the collider is part of (one bit per group).
  • The groups filter indicates what groups the collider can interact with (one bit per group).
info

Because the membership and filter bit masks are u32 there is a total of 32 groups. By default all bits are set to 1: the collider is part of every group, and can interact with every group.

For example, let's say we want our collider A to be part of the groups [0, 2, 3] and to be able to interact with the groups [2], then its groups membership is 0b1101 and its groups filter is 0b0100. The collision groups and solver groups of a collider can be set during or after its creation:

/* Set the collision groups and solver groups when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .collision_groups(InteractionGroups::new(
        Group::GROUP_1 | Group::GROUP_3 | Group::GROUP_4,
        Group::GROUP_3,
    ))
    .solver_groups(InteractionGroups::new(
        Group::GROUP_1 | Group::GROUP_2,
        Group::GROUP_1 | Group::GROUP_2 | Group::GROUP_4,
    ))
    .build();
/* Set the collision groups and solver groups after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_collision_groups(InteractionGroups::new(
    Group::GROUP_1 | Group::GROUP_3 | Group::GROUP_4,
    Group::GROUP_3,
));
collider.set_solver_groups(InteractionGroups::new(
    Group::GROUP_1 | Group::GROUP_2,
    Group::GROUP_1 | Group::GROUP_2 | Group::GROUP_4,
));
assert_eq!(
    collider.collision_groups(),
    InteractionGroups::new(
        Group::GROUP_1 | Group::GROUP_3 | Group::GROUP_4,
        Group::GROUP_3
    )
);
assert_eq!(
    collider.solver_groups(),
    InteractionGroups::new(
        Group::GROUP_1 | Group::GROUP_2,
        Group::GROUP_1 | Group::GROUP_2 | Group::GROUP_4
    )
);

After the broad-phase detects that two colliders A and B may start being in contact, the narrow-phase will check the collision groups of both colliders to see if it needs to compute contacts. The check operates as follows:

  • If the collider A is not member of any collision group in the filter of B, then no contact is computed.
  • If the collider B is not member of any collision group in the filter of A, then no contact is computed.
  • The exact bit-wise check is the following:
   (A.collision_groups().memberships & B.collision_groups().filter) != 0
&& (B.collision_groups().memberships & A.collision_groups().filter) != 0

If this test succeeds, then the narrow-phase will compute the contacts. Then it will check the solver groups of both colliders, using the same kind of tests as described before but using the solver_groups instead of collision_groups. If the test succeeds then the constraints solver will compute forces for these contacts. Otherwise, it won't.

Active collision types​

By default, collision-detection is completely disabled between two colliders when both are attached to non-dynamic bodies. Sometimes, it can be useful to enable collision-detection between, e.g., a collider attached to a kinematic rigid-body and a collider attached to a fixed rigid-body. This can be done by modifying the collider's ActiveCollisionTypes:

/* Set the active collision types when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .active_collision_types(
        ActiveCollisionTypes::default() | ActiveCollisionTypes::KINEMATIC_FIXED,
    )
    .build();
/* Set the active collision types after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_active_collision_types(
    ActiveCollisionTypes::default() | ActiveCollisionTypes::KINEMATIC_FIXED,
);
assert!(collider
    .active_collision_types()
    .contains(ActiveCollisionTypes::DYNAMIC_KINEMATIC));
assert!(collider
    .active_collision_types()
    .contains(ActiveCollisionTypes::KINEMATIC_FIXED));
info

To enable collision-detection between kinematic bodies and fixed bodies (as well as dynamic bodies), set its active collision types to:

ActiveCollisionTypes::default() | ActiveCollisionTypes::KINEMATIC_FIXED

Active events​

Event handlers are user-defined callbacks used to be notified when two colliders start/stop touching. By default no collision event is generated by the narrow-phase. In order to enable a collision event for a pair of colliders, at least one of the involved colliders must have the corresponding event set as active. An event is activated for a collider by setting its corresponding active events bit to 1:

  • Setting the ActiveEvents::COLLISION_EVENTS bit to 1 enables the collision events involving the collider.

The active events of a collider can be set when the collider is created or after its creation:

/* Set the active events when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .active_events(ActiveEvents::COLLISION_EVENTS)
    .build();
/* Set the active events after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.set_active_events(ActiveEvents::COLLISION_EVENTS);
assert!(collider
    .active_events()
    .contains(ActiveEvents::COLLISION_EVENTS));

Active hooks​

Physics hooks are user-defined callbacks used to filter-out some contact pairs, or modify contacts, based on arbitrary user code. In order to enable a physics hook for a pair of colliders, at least one of the involved colliders must have the corresponding hook set as active. A hook is activated for a collider by setting its corresponding active hooks bit to 1:

The active hooks of a collider can be set when the collider is created or after its creation:

/* Set the active hooks when the collider is created. */
let collider = ColliderBuilder::ball(0.5)
    .active_hooks(ActiveHooks::FILTER_CONTACT_PAIRS | ActiveHooks::MODIFY_SOLVER_CONTACTS)
    .build();
/* Set the active hooks after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider
    .set_active_hooks(ActiveHooks::FILTER_CONTACT_PAIRS | ActiveHooks::MODIFY_SOLVER_CONTACTS);
assert!(collider
    .active_hooks()
    .contains(ActiveHooks::FILTER_CONTACT_PAIRS));
assert!(collider
    .active_hooks()
    .contains(ActiveHooks::MODIFY_SOLVER_CONTACTS));

User-data​

Each collider can be given a user-defined data of type u128. This integer can have any value and is never used/modified by the physics-engine. This can for example be useful to add some custom data for personalized contact filtering/modification.

This user-data can be set when the collider is created or after its creation:

/* Set the user-data when the collider is created. */
let collider = ColliderBuilder::ball(0.5).user_data(42).build();
/* Set the user-data after the collider creation. */
let collider = collider_set.get_mut(collider_handle).unwrap();
collider.user_data = 42;
assert_eq!(collider.user_data, 42);